When Damsel took this photo of one of the cacti in the patio, it reminded me of a post I did back in the dark ages (still working for a living) about the Fibonacci Series:
When Damsel snapped this picture of a seashell a couple of days ago, it reminded me of a class I took in school. One segment of this class studied the mathematics of pattern formations in nature. It was interesting to me then and has been interesting since.
The phenomenon of an expanding spiral, as in the photo, comes from a number progression known as the Fibonacci series. The series is formed by starting with 0 and 1 and then adding the latest two numbers to get the next number in the progression. The first Fibonacci numbers are 0, 1, 1, 2, 3, 5, 8, 13, and so on.
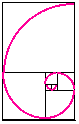If you stack squares of dimensions in the Fibonacci sequence and connect the base intersections with a smooth curve, you get a spiral that resembles that of the shell. In the diagram at the left, two squares of dimension 1 are located in the center of the spiral, and squares of 2, 3, 5, 8 and 13 are added to the rectangle stack.
A property of the Fibonacci series is that as the series progresses, the ratio of adjacent numbers converges on a quantity known as the Golden Ratio or Golden Section. Golden Ratio comes from a name given by renaissance mathematicians. It was probably Leonardo da Vinci who first called it the sectio aurea (Latin for the golden section). The Golden Ratio appears regularly in arts, in architecture and in nature.
For everything you ever wanted to know about the Fibonacci series numbers and the Golden Section, visit Dr Ron Knott’s multimedia web site.
UPDATE Fibonacci spirals in linear perspective: Observe the spiral staircase as it winds into the distance below. I found this picture on a website all about European architecture. I was looking for something else and noticed the Fibonacci connection.
I used to listen to a group called “IF”, and one of their song’s was called “Fibonacci’s Number”.
Mammillarias do have their tubercles arranged in Fibonacci spirals, but only so far as the tops of the cacti. Once the spirals curve off the top to go down the side, they don’t expand anymore, even though perspective (the staircase) could make it seem so. The shell could theoretically expand forever, though it stops when the animal dies.
It’s very interesting how the spirals are plotted based on the Golden Ratio (Phi). Each angle increases by incrementing 1/Phi and the radius is the square root of the point number. That’s how I plotted the planar spiral above using Excel.
Interesting stuff this nature – almost like someone engineered it.